Wahlteil 2017 – Analysis A 1 - Aufgabe A 1.1
Die Anzahl der Käufer einer neu eingeführten Smartphone-App soll modelliert werden.
Dabei wird die momentane Änderungsrate beschrieben durch die Funktion f mit
f(t)=6000·t·e-0,5t; t≥0
(t in Monaten nach der Einführung, f(t) in Käufer pro Monat).a) Zuerst werden nur die ersten zwölf Monate nach der Einführung betrachtet.
Geben Sie die maximale momentane Änderungsrate an.
Bestimmen Sie den Zeitraum, in dem die momentane Änderungsrate größer als 4000 Käufer pro Monat ist.
Bestimmen Sie die Zeitpunkte, zu denen die momentane Änderungsrate am stärksten abnimmt bzw. zunimmt.
(4,5 VP)
Lösung Aufgabe A 1.1a) Maximale momentane Änderungsrate
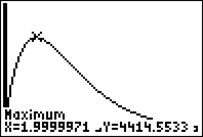
Geben Sie den Funktionsterm zunächst bei Y1 im Y-Editor des GTR ein und lassen Sie sich den Graphen im x-Intervall [0;12] und im y-Intervall [0;6000] zeichnen.
Anschließend können Sie mit 2ND CALC maximum das Maximum bestimmen und erhalten aufgerundet 4415.
Ergebnis: Die maximale momentane Änderungsrate beträgt 4.415 Käufer pro Monat.
Zeitraum für Änderungsrate ≥4000
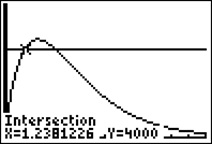
Für die nächste Teilaufgabe geben Sie im Y-Editor bei Y2 den konstanten Wert 4000 ein und lassen sich die beiden Graphen nochmals zeichnen.
Mit 2ND CALC intersect bestimmen Sie den linken und den rechten Schnittpunkt der beiden Graphen. Sie erhalten t1=1,24 und t2=3,02.
Ergebnis: Im Zeitraum zwischen 1,24 und 3,02 Monaten nach Einführung der App ist die momentane Änderungsrate größer als 4.000 Käufer pro Monat.
Stärkste Ab- und Zunahme der Änderungsrate
| Die stärkste Ab- bzw. Zunahme der momentanen Änderungsrate bekommen wir über den Tief- bzw. Hochpunkt der ersten Ableitung. Hierfür geben Sie im GTR bei Y1 den Ausdruck für die erste Ableitung ein und lassen Sie sich den Graphen zeichnen. | 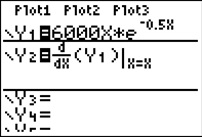 |
| Beachten Sie, dass es sich bei der stärksten Zunahme nicht um einen Wendepunkt handelt! Die stärkste Zunahme findet sich in der Ableitungskurve am linken Rand, da dort die Ableitung (also die Steigung von f(x)) den höchsten Wert hat. | 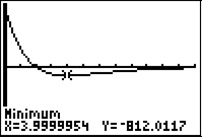 |
Ergebnis: Der Zeitpunkt der stärksten Abnahme liegt im vierten Monat nach Einführung der App, während die stärkste Zunahme gleich zu Beginn der Einführung stattfindet.
Wahlteil 2017 – Analysis A 2 - Aufgabe A 2.1
An einem Stausee wird der Zu- und Abfluss künstlich geregelt. Dabei wird die momentane Zuflussrate beschrieben durch die Funktion z mit
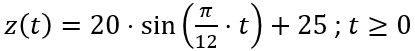
a(t)=19; t≥0
(t in Stunden seit Beobachtungsbeginn, z(t) und a(t) in m3/h)a) Zunächst werden die ersten 24 Stunden nach Beobachtungsbeginn betrachtet.
Bestimmen Sie die minimale momentane Zuflussrate.
In welchem Zeitraum nimmt die Wassermenge im Stausee ab?
Bestimmen Sie die maximale momentane Änderungsrate der Wassermenge.
(4 VP)
Lösung Aufgabe A 2.1
a) Minimale momentane Zuflussrate
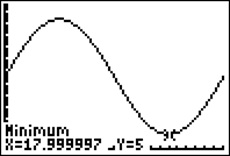
Geben Sie den Funktionsterm von z(t) bei Y1 im GTR ein und lassen Sie sich den Graphen im x-Intervall [0;24] und im y-Intervall [0;50] zeichnen. (Modus = RADIAN). Mit 2ND CALC minimum findet man x=18 und y=5. Da in 1000 m3/h gemessen wird haben wir als
Ergebnis: Die minimale momentane Zuflussrate beträgt 5.000 m3/h.
Zeitraum, in dem die Wassermenge abnimmt
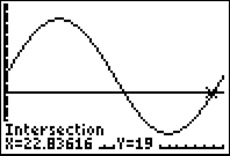
Die Wassermenge im Stausee nimmt ab, wenn die Zuflussrate kleiner ist als die Abflussrate. Geben Sie hierfür zunächst den Wert 19 (also die Abflussrate) bei Y2 im GTR ein und lassen Sie sich die beiden Graphen erneut zeichnen. Mit 2ND CALC intersect bestimmen Sie die beiden Schnittpunkte bei t1≈13,16 und t2≈22,84. Zwischen t1 und t2 liegt die Zuflussrate unterhalb der Abflussrate.
Ergebnis: Zwischen 13,16 und 22,84 Stunden nach Beobachtungsbeginn nimmt die Wassermenge im Stausee ab.
Maximale momentane Änderungsrate
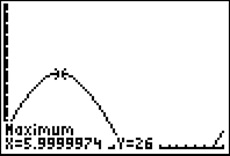
Die Änderungsrate ist gegeben durch Zufluss minus Abfluss also durch
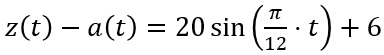
Ergebnis: Die maximale Änderungsrate wird 6 Stunden nach Beobachtungsbeginn erreicht und beträgt dann 26.000 m3/h.
Wahlteil 2016 – Analysis A 1 - Aufgabe A 1.1
Der Graph der Funktion f mit f(x)=-0,1x3+0,5x2+3,6 beschreibt modellhaft für -1≤x≤5 das Profil eines Geländequerschnitts.
Die positive x-Achse weist nach Osten, f(x) gibt die Höhe über dem Meeresspiegel an
(1 Längeneinheit entspricht 100 m).
a) Auf welcher Höhe liegt der höchste Punkt des Profils?
In dem Tal westlich dieses Punktes befindet sich ein See, der im Geländequerschnitt an seiner tiefsten Stelle 10 m tief ist.
Bestimmen Sie die Breite des Sees im Geländequerschnitt.
Ab einer Hangneigung von 30° besteht die Gefahr, dass sich Lawinen lösen.
Besteht an der steilsten Stelle des Profils zwischen See und höchstem Punkt Lawinengefahr?
(5 VP)
Lösung Aufgabe A 1.1a) Höchster Punkt des Profils
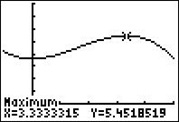
Wenn Sie den Funktionsterm im GTR bei Y1 eingeben, können Sie mit 2ND CALC maximum den höchsten Punkt im Geländeprofil bestimmen, siehe Abbildung rechts.
Beachte: 1 LE entspricht 100 m.
Ergebnis: 333 m östlich des Ursprungs hat das Gelände eine Höhe von 545 m über dem Meeresspiegel. Dies ist der höchste Punkt im Geländeprofil.
Breite des Sees
| Wir bestimmen zunächst mit dem GTR über 2ND CALC minimum den tiefsten Punkt im Gelände und erhalten T(0|3,6). Der Wasserspiegel des Sees liegt 10 m über diesem Punkt, das sind 0,1 Längeneinheiten über 3,6. | 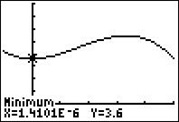 |
| Wenn wir nun mit dem GTR eine Gerade bei y=3,7 zeichnen lassen, können wir mit 2ND CALC intersect die Schnittpunkte dieser Geraden mit dem Graphen bestimmen. Sie erhalten x1=-0,43 und x1=0,47. | 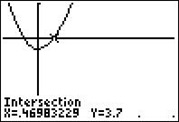 |
| Die Breite des Sees beträgt somit 0,47-(-0,43)=0,9 LE also 90 m. |  |
Ergebnis: Der See ist ca. 90 m breit.
Besteht Lawinengefahr?
| Die steilste Stelle zwischen dem See und dem höchsten Punkt ist der Wendepunkt W. Wir bestimmen W mit dem GTR indem wir den Graphen der Ableitung zeichnen lassen (Einstellungen siehe Abbildung rechts). | 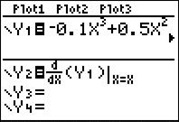 |
| Die x-Koordinate des Maximums im Graphen von f' ist diejenige des Wendepunkts, nämlich x=1,67. An dieser Stelle gilt f' den Wert 0,83 (siehe Abbildung). Dies ist der Wert der Steigung im Wendepunkt. Wenn Sie den GTR in den DEGREE-Modus schalten, können Sie den Steigungswinkel mit 2ND tan(0.83333) bestimmen und erhalten α≈39,8°. | 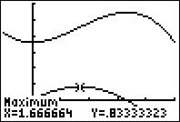 |
Ergebnis: Der Steigungswinkel an der steilsten Stelle zwischen See und höchstem Punkt ist größer als 30°. Somit besteht Lawinengefahr!
Wahlteil 2016 – Analysis A 2 - Aufgabe A 2.1
In einem Skigebiet beträgt die Schneehöhe um 10.00 Uhr an einer Messstelle 150 cm. Die momentane Änderungsrate dieser Schneehöhe wird beschrieben durch die Funktion s mit
s(t)=16e-0,5t-14e-t-2; 0≤t≤12
(t in Stunden nach 10.00 Uhr, s(t) in Zentimeter pro Stunde).a) Bestimmen Sie die maximale momentane Änderungsrate der Schneehöhe.
Ermitteln Sie den Zeitraum, in dem die momentane Änderungsrate der Schneehöhe größer als
2 cm pro Stunde ist.
Wie hoch liegt der Schnee um 12.00 Uhr?
(4 VP)
Lösung Aufgabe A 2.1a) Maximale momentane Änderungsrate der Schneehöhe
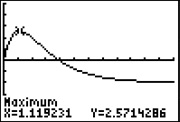
Geben Sie den Funktionsterm bei Y1 im GTR ein, und lassen Sie sich den Graphen im x-Intervall [0;12] und im y-Intervall [-5;5] zeichnen. Mit 2ND CALC maximum bestimmen Sie den höchsten Punkt. Sie erhalten die Stelle x=1,12 mit einer momentanen Änderungsrate von y=2,57, siehe Abbildung rechts.
Ergebnis: Die maximale momentane Änderungsrate beträgt 2,57 cm pro Stunde.
Zeitraum in dem die momentane Änderungsrate der Schneehöhe größer als 2 cm pro Stunde ist
| Hierfür lassen wir uns mit dem GTR eine waagrechte Gerade bei y=2 zeichnen (einfach bei Y2 den Wert 2 eingeben). Mit 2ND CALC intersect bestimmen Sie die beiden Schnittpunkte mit der Kurve. Sie erhalten x1=0,51 bzw. x2=1,99, siehe Abbildungen rechts. | 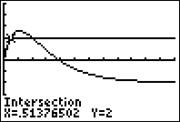 |
| Da x in Stunden nach 10.00 Uhr gemessen wird, haben wir folgendes | 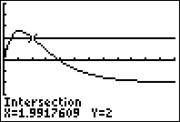 |
Ergebnis: Etwa zwischen 10.30 Uhr und 12.00 Uhr ist die momentane Änderungsrate größer als 2 cm pro Stunde.
Wie hoch liegt der Schnee um 12.00 Uhr?
Über das Integral
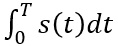 lässt sich der gesamte Höhenzuwachs des Schnees nach T Stunden ermitteln.
Für die Gesamthöhe nehmen wir noch die Anfangshöhe, nämlich 150 cm, hinzu und erhalten
lässt sich der gesamte Höhenzuwachs des Schnees nach T Stunden ermitteln.
Für die Gesamthöhe nehmen wir noch die Anfangshöhe, nämlich 150 cm, hinzu und erhalten
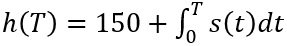 Um 12.00 Uhr haben wir 2 Stunden nach 10.00 Uhr, d.h. wir müssen für T den Wert 2 einsetzen (und nicht 12!).
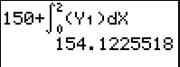
Das Integral geben Sie dann wie rechts stehend gezeigt im GTR ein.
Um 12.00 Uhr haben wir 2 Stunden nach 10.00 Uhr, d.h. wir müssen für T den Wert 2 einsetzen (und nicht 12!).
Das Integral geben Sie dann wie rechts stehend gezeigt im GTR ein.Ergebnis: Um 12.00 Uhr liegt der Schnee etwa 154,1 cm hoch.
| Downloads |
PowerPoint